RESEÑA HISTORICA
Los egipcios dieron origen por primera vez a las fracciones comunes alrededor del año1000a.C; alrededor del 500 a.C un grupo de matemáticos griego liderados por pitagoras se dio cuenta de la necesidad de los numeros iiracionales . Los numeros negativos fueron ideados por matemáticos indios cerca del 600, posiblemente reinventados a china poco después, pero no se utilizaron en europa hasta el siglo XVII, si bien a finales del XVIII Leonhard Euler descartó las soluciones negativas de las ecuaciones porque las consideraba irreales. En ese siglo, en el calculo se utilizaban números reales sin una definición precisa, cosa que finalmente sucedió con la definición rigurosa hecha por Georg Cantor en 1871.
En realidad, el estudio riguroso de la construcción total de los números reales exige tener amplios antecedentes de teorias de conjuntos y logica matematica . Fue lograda la construcción y sistematización de los números reales en el siglo XIX por dos grandes matemáticos europeos utilizando vías distintas: la teoría de conjuntos de Georg Cantor (encajamientos sucesivos, cardinales finitos e infinitos), por un lado, y el análisis matemático de Richard Dedekind (vecindades, entornos y cortaduras de Dedekind).
NUMEROS REALES COMO UN CAMPO
Al "construir" la matemática, los números naturales, son una clase de equivalencia de conjuntos coordinables. Los números enteros son una clase de equivalencia de parejas ordenadas de números naturales. Los números racionales son una clase de equivalencia de parejas ordenadas de números enteros.
Los números irracionales son los elementos de la recta real que NO pueden expresarse mediante el cociente de dos enteros y se caracterizan por poseer infinitas cifras decimales que no siguen un periodo definido.
De este modo ya pueden definirse los números reales que surgen de la unión de lo que son los conjuntos de números naturales, enteros, irracionales y racionales.
Los números reales son llamados campo de los números reales. Esto es por que son un grupo abeliano, es decir poseen la ley de cerradura, la conmutativa, asociativa, distributiva y poseen elementos neutros e inversos. Todos estos elementos hacen que los números reales sean un campo.
AXIOMAS DE NUMEROS REALES
ara que todos los procedimientos matemáticos usados sean válidos se debe partir de una base que respalde cada procedimiento, cada paso lógico usado, y debe, en consecuencia, demostrarse cada afirmación no trivial. Son estas demostraciones los pilares fundamentales de toda rama de las matemáticas, ya que sin ellos puede ponerse en duda la veracidad de cualquier afirmación.
Las afirmaciones a las que se hace referencia se llaman axioma. Serán, por lo tanto, afirmaciones que se aceptan como verdaderas debido a su trivialidad, pudiendo en ocasiones ser demostradas cuando no lo son.
El otro tipo de afirmaciones a las que se hace referencia diciendo: "afirmacion no trivial", son los teoremas , que son ya, afirmaciones no tan triviales y muchas veces poco intuitivas. Estas afirmaciones deben ser demostradas usando los axiomas u otros teoremas ya demostrados. Una consecuencia inmediata de un teorema se llamará corolario.
Hay tres tipos de axiomas:
- Los axiomas algebraicos
- Los axiomas de orden
- El axioma topológico.
Axioma de los números reales (suma y resta)
Ley de cerradura
Axioma conmutativo
Axioma asociativo
Axioma distributivo
Axioma del elemento neutro
Axioma del elemento inverso
Axioma del numero inverso
TEOREMAS DE NUMEROS REALES
A
partir de los axiomas de R, los axiomas de orden y de las definiciones
mostraremos algunas de las propiedades de los reales demostrándolas como
teoremas que nos servirán para entender la naturaleza y comportamiento
de este conjunto de números.
TEOREMA 1
En los números reales se cumplen las leyes cancelativas y uniforme con la suma, es decir:
Si x+y=x+z entonces y=z.
Si y=z entonces x+y=x+z.
Demostración/:
y = 0+y
y = ((-x)+x)+y
y = (-x)+(x+y)
y=(-x)+(x+z)
y =(-x)+(x+z)
y=((-x)+x)+z
y= =0+z
y==z
la
anterior demostración se justifica usando el axioma 4, el axioma 5, ley
asociativa, la hipótesis, ley asociativa, el axioma 5 y el axioma 4
respectivamente.
Por ley reflexiva x+z=x+z pero como z=y entonces por ley transitiva x+z= x+y.
TEOREMA 2
Los neutros e inversos aditivos y multiplicativos son únicos.
Los neutros e inversos aditivos y multiplicativos son únicos.
Demostración/:
Supongamos que existen 01 y 02 dos neutros aditivos, entonces 01 + 02 = 01 y 02 +01 = 02 luego por ley transitiva y conmutativa 01= 01 + 02=02 +01 = 02.luego estos neutros aditivos son el mismo. (Análogamente se demuestra para el neutro multiplicativo).
Ahora supongamos que para x hay dos inversos aditivos x1 y x2 tal que x+ x1 = 0 y x+ x2 = 0 por ley transitiva tenemos que x+ x1 = x+ x2 luego por ley cancelativa x1 = x2. Luego los inversos aditivos para x real son el mismo. (Análogamente se demuestra para el inverso multiplicativo teniendo en cuenta que x≠0).
TEOREMA 3
En los números reales distintos de cero se cumplen las leyes cancelativas y uniforme con la multiplicación, es decir:
Ahora supongamos que para x hay dos inversos aditivos x1 y x2 tal que x+ x1 = 0 y x+ x2 = 0 por ley transitiva tenemos que x+ x1 = x+ x2 luego por ley cancelativa x1 = x2. Luego los inversos aditivos para x real son el mismo. (Análogamente se demuestra para el inverso multiplicativo teniendo en cuenta que x≠0).
TEOREMA 3
En los números reales distintos de cero se cumplen las leyes cancelativas y uniforme con la multiplicación, es decir:
SI x•y=x•z entonces y=z.
Si y=z entonces x•y=x•z.
Demostración/:La demostacion es analoga a la del Teorema1.
TEOREMA 4
TEOREMA 4
-0=0.
Demostración/:Tenemos que 0+(-0) = 0 y 0+0 = 0 luego por ley transitiva 0+(-0) = 0+0, finalmente por ley cancelativa 0 = -0.
TEOREMA 5
Para x real se cumple: -(-x)= x.
TEOREMA 5
Para x real se cumple: -(-x)= x.
Demostración/:
–(-x) = 0+(–(-x))=(x+(-x))+ (–(-x))= x+((-x)+ (–(-x)))= x+0=x.Podemos ver que usamos los axiomas 4 y 5 y el hecho de que (–(-x)) es el inverso aditivo de (-x).
LEMA
Para toda x real se cumple: x•0=0•x=0.
Demostración/:
x•0=x• (0+0) = x•0+x•0, luego x•0 = x•0+x•0 y por ley cancelativa 0 = x•0 ò x•0=0, de la misma forma demostramos que 0•x=0, por lo que concluimos que x•0=0•x=0.
Demostración/:
x•0=x• (0+0) = x•0+x•0, luego x•0 = x•0+x•0 y por ley cancelativa 0 = x•0 ò x•0=0, de la misma forma demostramos que 0•x=0, por lo que concluimos que x•0=0•x=0.
TEOREMA 6
Para x, y reales se cumple: (-x) •y= x•(-y) = -(x•y).
Demostración/:
Por lema 0=0•y=(x+(-x)) 0•y = x•y+(-x) •y, entonces 0= x•y+(-x)•y y por ley uniforme se puede sumar -(x•y) y tenemos que -(x•y) = (-(x•y))+x•y+(-x)•y luego (x•y))+x•y=0 por lo que se tiene que: -(x•y) = 0+(-x)•y =+(-x)•y. Analogamente se demuestra que x•(-y)= -(x•y).
Por lema 0=0•y=(x+(-x)) 0•y = x•y+(-x) •y, entonces 0= x•y+(-x)•y y por ley uniforme se puede sumar -(x•y) y tenemos que -(x•y) = (-(x•y))+x•y+(-x)•y luego (x•y))+x•y=0 por lo que se tiene que: -(x•y) = 0+(-x)•y =+(-x)•y. Analogamente se demuestra que x•(-y)= -(x•y).
TEOREMA 7
Para x≠0 real se cumple: 1/(1/x)= x.
Demostración/:
Esta demostracion es parecida al adel teorema 5.
TEOREMA 8
Para x, y reales distintos de cero se cumple: 1/(x•y)= (1/x)•(1/y).
TEOREMA 8
Para x, y reales distintos de cero se cumple: 1/(x•y)= (1/x)•(1/y).
Demostración/:
1/(x•y)=1•1•1/(x•y)
1/(x•y)= (x•(1/x)) • (y•(1/y))•1/(x•y)
1/(x•y)= (x•y) • ((1/x)•(1/y))•1/(x•y)
1/(x•y)=((1/x)•(1/y))• ((x•y) • 1/(x•y))
1/(x•y)= (1/x)•(1/y).Aquí hemos usando en repetidas ocasiones propiedades como la ley conmutativa y asociativa para el producto y la existencia de los neutros e inversos multiplicativos.
TEOREMA 9
Para x, y reales distintos de cero se cumple: 1/(x/y)= y/x.
1/(x•y)= (x•(1/x)) • (y•(1/y))•1/(x•y)
1/(x•y)= (x•y) • ((1/x)•(1/y))•1/(x•y)
1/(x•y)=((1/x)•(1/y))• ((x•y) • 1/(x•y))
1/(x•y)= (1/x)•(1/y).Aquí hemos usando en repetidas ocasiones propiedades como la ley conmutativa y asociativa para el producto y la existencia de los neutros e inversos multiplicativos.
TEOREMA 9
Para x, y reales distintos de cero se cumple: 1/(x/y)= y/x.
Demostración/:
Aquí vemos como los Teoremas 7 y 8 son usados junto con las propiedades conmutativa y asociatativa del producto para demostrar lo requerido.
Aquí vemos como los Teoremas 7 y 8 son usados junto con las propiedades conmutativa y asociatativa del producto para demostrar lo requerido.
1/(x/y)= 1/(x •(1/y))=(1/x)•(1/(1/y))=(1/x) •y = y/x.
TEOREMA 10
Para x, z reales y w, y reales distintos de cero se cumple: x/y + z/w = (x•w+ z•y)/ y•w.
Demostración/:
(x/y)+(z/w)= (x/y+z/w)•1
(x/y)+(z/w)= (x/y+z/w)•((y•w)(1/y•w))
(x/y)+(z/w)= ((x/y+z/w)(y•w))(1/y•w)
(x/y)+(z/w)= (x/y• (y•w)+z/w• (y•w))(1/y•w)
(x/y)+(z/w)= (x•w+ y•z)(1/y•w)
(x/y)+(z/w)= (x•w+ y•z)/(y•w)
Note que en esta demostración usamos los axiomas 2, 3, 6 y 7.
(x/y)+(z/w)= (x/y+z/w)•1
(x/y)+(z/w)= (x/y+z/w)•((y•w)(1/y•w))
(x/y)+(z/w)= ((x/y+z/w)(y•w))(1/y•w)
(x/y)+(z/w)= (x/y• (y•w)+z/w• (y•w))(1/y•w)
(x/y)+(z/w)= (x•w+ y•z)(1/y•w)
(x/y)+(z/w)= (x•w+ y•z)/(y•w)
Note que en esta demostración usamos los axiomas 2, 3, 6 y 7.
TEOREMA 11
Para x, z reales y w, y reales distintos de cero se cumple: (x/y)• (z/w)= (x•z)/ (y•w).
Demostración/:
Al igual que en el teorema anterior aquí usamos la definición 5 los axiomas 2, 3 y los teoremas 8 y 9 .
(x/y)•(z/w)=((x/y)•z)/w
(x/y)•(z/w)= ((x•(1/y))•z)/w
(x/y)•(z/w)= (x•((1/y)•z)/w
(x/y)•(z/w)= (x•(z/y))/w
(x/y)•(z/w)= ((x•z)/y)/w
(x/y)•(z/w)= x•z/y•w.
(x/y)•(z/w)=((x/y)•z)/w
(x/y)•(z/w)= ((x•(1/y))•z)/w
(x/y)•(z/w)= (x•((1/y)•z)/w
(x/y)•(z/w)= (x•(z/y))/w
(x/y)•(z/w)= ((x•z)/y)/w
(x/y)•(z/w)= x•z/y•w.
TEOREMA 12
Para x, y y z reales se cumple: x>y si y solo si x+z>y+z.
Demostración/:
Sea a= x+z y b= y+z, entonces a-b=(x+z)-(y+z)=x-y como a>b si y solo si a-b>0 y por transitividad de a>b se deduce que x+z>y+z.Por otro lado veamos que x+z > y+z si y solo si (x+z)-(y+z) >0 luego x-y >0 x>y.
Sea a= x+z y b= y+z, entonces a-b=(x+z)-(y+z)=x-y como a>b si y solo si a-b>0 y por transitividad de a>b se deduce que x+z>y+z.Por otro lado veamos que x+z > y+z si y solo si (x+z)-(y+z) >0 luego x-y >0 x>y.
TEOREMA 13
Para x, y y z reales con z distinto de cero se cumple:
x>y si y solo si x•z>y•z con z>0.
x>y si y solo si y•z > x•z con 0>z.
Demostración/:
Demostración/:
Si x>y si y solo si x-y >0 por lo tanto x-y es positivo, si z>0 entonces z tambian es positivo y por los axiomas de orden vemos que (x-y)•z es positivo si y solo si (x-y)•z >0Si y solo si x •z -y•z>0 si y solo si x •z >y•z.
Si x>y si y solo si x-y >0 por lo tanto x-y es positivo, 0>z entonces (-z)>0 usando el mismo razonamiento que en i) llegamos a que y•z-x•z>0 si y solo si y•z >x•z.ii) se deduce de la misma forma.
Si x>y si y solo si x-y >0 por lo tanto x-y es positivo, 0>z entonces (-z)>0 usando el mismo razonamiento que en i) llegamos a que y•z-x•z>0 si y solo si y•z >x•z.ii) se deduce de la misma forma.
TEOREMA 14
Para x, y reales distintos de cero se cumple:
Para x, y reales distintos de cero se cumple:
i) SI x•y>0 con x>0 entonces y>0.
ii) Si x•y>0 con 0>x entonces 0>y.
iii) Si 0> x•y con x>0 entonces 0>y.
iv) Si 0> x•y con 0>x entonces y>0.
Demostración/:Supongamos que no se cumple la tesis, es decir, 0>y como x>0 entonces por teorema 13 0>x•y llegando a la contradicción de la hipótesis o sea que lo afirmamos anteriormente es falso, llegando a la demostración del teorema (análogamente se demuestra para ii),iii) y iv).
TEOREMA 15
Para x≠0 real se cumple: x²>0 .
Demostración/:
Si x>0 entonces x es positivo luego x•x=x² es positivo si y solo si x²>0.Si 0>x entonces (-x) es positivo luego (-x)•(-x)=(-x)² es positivo si y solo si (-x)²>0.Pero (-x)•(-x)=-(x•(-x))=-(-(x•x))=x•x=x² por teorema 6, con lo que vemos que (-x)•(-x)= x²>0.
TEOREMA 16
Para x≠0 real se cumple:
i) x>0 si y solo si (1/x)>0.
ii) 0>x si y solo si 0>(1/x).
TEOREMA 16
Para x≠0 real se cumple:
i) x>0 si y solo si (1/x)>0.
ii) 0>x si y solo si 0>(1/x).
Demostración/:
Como x>0; x≠0 entonces existe (1/x), luego x•(1/x)=1 entonces.x>0 implica que x•1>0 si y solo si x• (x•(1/x)) >0, luego x²•(1/x )>0 y como x²>0 por teoremas 13 y 14 se deduce que 1/x>0.
Por otro lado 1/x>0; x≠0 entonces existe x, luego x•(1/x)=1 entonces.1/x>0 implica que (1/x)•1>0 si y solo si (1/x)• ((1/x)•x)) >0, luego (1/x)²•x>0 y como (1/x)²>0 por teoremas 13 y 14 se deduce que x>0.
Por otro lado 1/x>0; x≠0 entonces existe x, luego x•(1/x)=1 entonces.1/x>0 implica que (1/x)•1>0 si y solo si (1/x)• ((1/x)•x)) >0, luego (1/x)²•x>0 y como (1/x)²>0 por teoremas 13 y 14 se deduce que x>0.
RAZONES Y PROPORCIONES
RAZONES
Se llama razón entre dos números reales distintos de cero, dados en un cierto orden, al cociente exacto del primer por el segundo. El primero se llama antecedente y el segundo consecuente.
En los símbolos: la razón entre a y b es a/b = a : b siendo a y b números reales.
Ejemplos: La razón entre 8 y 4 es 8/4 = 2
PROPORCIONES
Se forma una proporción, cuando la razón entre los dos números primeros es igual a la razón entre los dos últimos.
En símbolos: Dados a, b, c y d si a/b = c/d, a, b, c y d forman una proporción y se lee “a es ab como c es a d” Ejemplos: -1/0.5 = -8/4 es una proporción pues -1/0.5 = -2 y -8/4 = -2
PROPIEDADES DE LAS PROPORCIONES
Propiedad 1 :
toda proporcion , la suma o diferencia entre el antecedente y el consecuente de la primera razón es a su consecuente , como la suma o diferencia entre el antecedente y el consecuente de la segunda razón es a su consecuente .
a = c → a + b = c + d
b d b d
a = c → a - b = c - d
b d b d
Propiedad 2 :
en toda proporción , la suma o diferencia entre el antecedente y el consecuente de la primera razón es a su antecedente , como la suma o diferencia entre el antecedente y el consecuente de la segunda razón es a su antecedente .
a = c → a + b = c + d
b d a c
a = c → a - b = c - d
b d a c
Propiedad 3 :
en toda proporción, la suma entre el antecedente y el consecuente de la primera razón es a la diferencia entre los mismos , como la suma entre el antecedente y el consecuente de la segunda razón es a la diferencia de los mismos .
a = c → a + b = c + d
b d a - b c - d
Serie de razones iguales : una serie de razones o iguales es una igualdad entre dos o más razones .
a = c = e = m
b d f n
Propiedad 4 :
en toda serie de razones iguales la suma de los antecedentes es a la suma de los consecuentes , como uno de los antecedentes es a su consecuente .
a = c = e = m = a + c + e+ m
b d f n b+ d + f+ n
Ejercicio 1
Hallar los valores desconocidos de la siguiente serie de razones iguales .
4 = 5 = 1 ↔ 4 = 1 → 4 . 3 = b . 1 → b = 12
b d 3 b 3
5 = 1 → 5 . 3 = 1 . d → d = 15
d 3
4 = 5 = 1 ↔ 4 = 5 = 1
b d 3 12 15 3
Ejercicio 2 . Aplicar las propiedades de las proporciones .
a) a+ b = 9 ; a / b = 1 / 2
a = c → a + b = c + d
b d b d
9 = 1 + 2 → 9 = 3 → 9 . 2 = 3 . b → b = 9 . 2 = 6
b 2 b 2 3
a + b = 9
a + 6 = 9 ↔ a = 9 - 6 → a = 3
b) a - b = 2 ; a / b = 4 /3
a = c → a - b = c - d
b d a c
2 = 4 - 3 → 2 = 1 → 2 . 4 = a . 1 → a = 2 . 4 = 8
a 4 a 4 1
a - b = 2
8 - b = 2 ↔ b = 8 - 2 = 6
INTERVALOS
es el conjunto de todos los numeros que estan entre a y b en donde a y b son los extremos.
CLASIFICACION DE INTERVALOS
Se pueden clasificar los intervalos según sus características topologicas (intervalos abiertos, cerrados, semiabiertos) o según sus características metricas (longitud: nula, finita no nula, infinita).
| Notación | Intervalo | Longitud | Descripción | |||
|---|---|---|---|---|---|---|
![[a, b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) |
 |
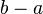 |
Intervalo cerrado de longitud finita. | |||
 |
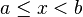 |
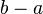 |
Intervalo semiabierto (cerrado en a, abierto en b). | |||
![]a, b] \ \ \mathrm{ \acute o } \ \ (a, b] \!](https://upload.wikimedia.org/math/0/1/8/0189f84b7a0ea78dbc527c545d8c9598.png) |
 |
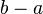 |
Intervalo semiabierto (abierto en a, cerrado en b). | |||
![]a, b[ \ \ \mathrm{ \acute o } \ \ (a, b) \!](https://upload.wikimedia.org/math/1/0/d/10d97baef8714cd0982a87681cfe4d1f.png) |
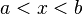 |
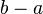 |
Intervalo abierto. | |||
![]-\infty, b[ \ \ \mathrm{ \acute o } \ \ (- \infty, b) \!](https://upload.wikimedia.org/math/0/9/7/097e7c70e6cbf2559d82fcb85f853033.png) |
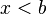 |
 |
Intervalo semiabierto. | |||
![]-\infty, b] \ \ \mathrm{ \acute o } \ \ (- \infty, b] \!](https://upload.wikimedia.org/math/e/8/2/e82cc38f6052cb558df6d0be418c5659.png) |
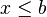 |
 |
Intervalo semiabierto. | |||
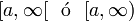 |
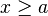 |
 |
Intervalo semiabierto. | |||
![]a, \infty [ \ \ \mathrm{ \acute o } \ \ (a, \infty ) \!](https://upload.wikimedia.org/math/8/e/6/8e62b6ce3cbde6646d2cd2dda6a5b6bc.png) |
 |
 |
Intervalo semiabierto. | |||
![]\infty, + \infty [ \ \ \mathrm{ \acute o } \ \ (\infty, + \infty ) \!](https://upload.wikimedia.org/math/6/b/a/6ba8dc9071eaad7acf515f333bba45cf.png) |
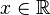 |
 |
Intervalo a la vez abierto y cerrado. | |||
 |
 |
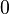 |
Intervalo cerrado de longitud nula (intervalo degenerado). | |||
 |
sin elemento | cero | conjunto vacio Intervalo abierto (a,a). |
OPERACIONES CON INTERVALO
Y el conjunto B:
El conjunto unión de A y B sería:
El conjunto intersección de A y B no existe:
El conjunto intersección de A y C es:
ECUACIONES
una ecuacion es aquella que es verdadera solo para algun o algunos valores de las variables del conjunto referencial que corresponda .
CLASIFICACION DE LAS ECUACIONES
Ecuaciones polinómicas enteras
Las ecuaciones polinómicas son de la forma P(x) = 0 , donde P(x) es un polinomio.
Grado de una ecuación
El grado de una ecuación es el mayor de los grados de los monomios que forman sus miembros.
Tipos de ecuaciones polinómicas
1. Ecuaciones de primer grado o lineales
Son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adoptan esa expresión.
(x + 1)2 = x2 - 2
x2 + 2x + 1 = x2 - 2
2x + 1 = -2
2x + 3 = 0
2. Ecuaciones de segundo grado o cuadráticas
una ecuacion cuadratica de esgundo grado que se puede representar con un predicado de la forma :
ax2 + bx + c = 0, con a ≠ 0.
Ecuaciones de segundo grado incompletas
ax2 = 0
ax2 + b = 0
ax2 + bx = 0
3. Ecuaciones de tercer grado
Son ecuaciones del tipo ax3 + bx2 + cx + d = 0, con a ≠ 0.
4. Ecuaciones de cuarto grado
Son ecuaciones del tipo ax4 + bx3 + cx2 + dx + e = 0, con a ≠ 0.
Ecuaciones bicuadradas
Son ecuaciones de cuarto grado que no tiene términos de grado impar.
ax4 + bx2 + c = 0, con a ≠ 0.
5. Ecuaciones de grado n
En general, las ecuaciones de grado n son de la forma:
a1xn + a2xn-1 + a3xn-2 + ...+ a0 = 0
Ecuaciones polinómicas racionales
Las ecuaciones polinómicas son de la forma  , donde P(x) y Q(x) son polinomios.
, donde P(x) y Q(x) son polinomios.
Ejemplos
 , donde P(x) y Q(x) son polinomios.
, donde P(x) y Q(x) son polinomios.
PROCESO DE RESOLUCION DE LAS ECUACIONES
1.- Agrupar en un miembro los términos con variables y en el otro los términos que no tienen variables.
(al pasar un término de un miembro a otro se pasa realizando la operación inversa)
2.- Resolver las operaciones que se indiquen en los miembros de manera independiente.
(Las operaciones se resuelven respetando el orden operacional)
| Ecuación | Pasos para resolver la ecuación |
 |
Se agrupan en un miembro los términos con variables y en el otro miembro los términos sin varibles.
Se resuelven las operaciones que se indiquen en los miembros de manera independiente.
Se despeja la variable y se resuelven las operaciones indicadas.
|
Pasos para comprobar soluciones en la ecuación
1.- Sustituir el valor de la variable en la ecuación original.
2.- Calcular cada miembro por separado.
3.- Comparar el resultado de ambos miembros.
(Si la proposición es verdadera, entonces el resultado obtenido es la solución de la ecuación.)
4.- Escribir el conjunto solución.
Comprobación

INECUACIONES
Una inecuacion es una desigualdad que relaciona letras y números mediante las operaciones aritméticas. Las letras se llaman incognitas.
Las soluciones de una inecuación son los valores que pueden tomar las incógnitas de manera que al sustituirlos en la inecuación hacen que la desigualdad sea cierta.
ejemplo:
En la inecuación 2x + 1 > 9, ¿qué valores pueden tomar las incógnitas para que la inecuación sea cierta?
Damos valores arbitrarios a la incógnita x, obteniendo:
Para x = 1: 2 · 1 + 1 = 3 < 9
Para x = 2: 2 · 2 + 1 = 5 < 9
Para x = 3: 2 · 3 + 1 = 7 < 9
Para x = 4: 2 · 4 + 1 = 9
Para x = 5: 2 · 5 + 1 = 11 > 9
Por tanto, la inecuación es cierta cuando sustituimos x por un número mayor que 4. La solución es x > 4.
CLASIFICACION DE LAS ECUACIONES
Los criterios más comunes de clasificación del ejemplo:
 .
.-
- De dos incógnitas. Ejemplo:
 .
. - De tres incógnitas. Ejemplo:
 .
. - etc.
- De dos incógnitas. Ejemplo:
- Según la potencia de la incógnita,
- De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo:
 .
. - De segundo grado o cuadrática. Cuando el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo:
 .
. - De tercer grado o cúbica. Cuando el mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo:
 .
. - etc.
- De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo:
Inecuaciones de segundo grado con una incógnita
Se expresan a través de cualquiera de las desigualdades siguientes (con a, b y c números reales, y a distinto de cero):Sistema de inecuaciones
Véase también: programacion lineal
La región de viabilidad en un problema de programacion lineal está definida por un sistema de inecuaciones.
Sistema de inecuaciones de primer grado con una incógnita
Es un conjunto de inecuaciones de primer grado con la misma variable:La solución del sistema será el conjunto de números reales que verifican a la vez todas las inecuaciones.
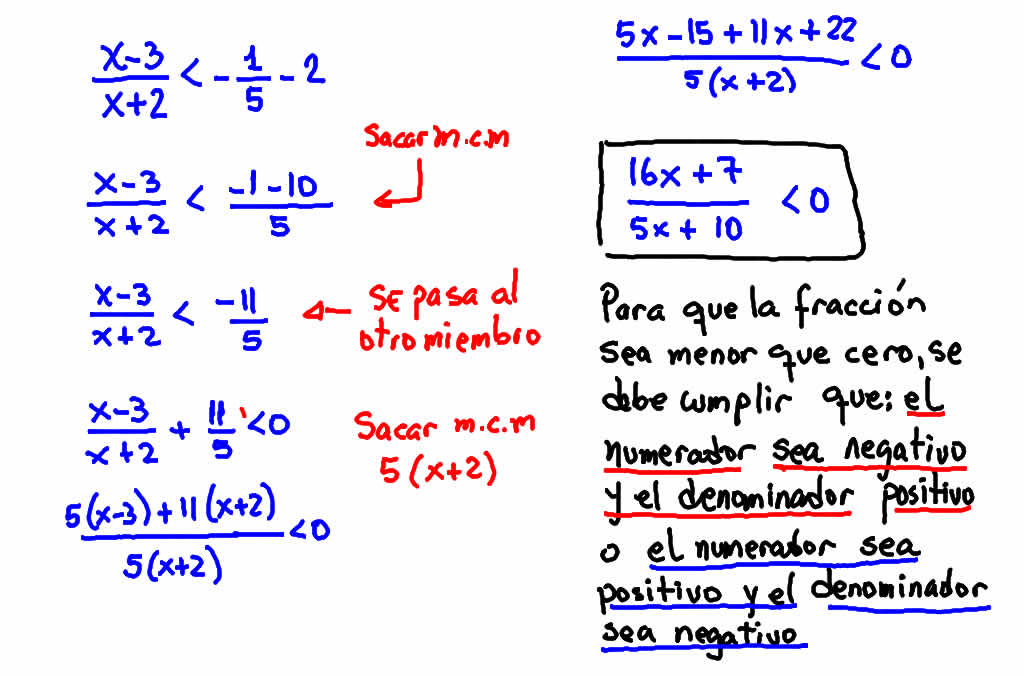
PROCESO DE RESOLUCION DE INECUACIONES
ejemplo:
ejemplo:
En la inecuación 2x + 1 > 9, ¿qué valores pueden tomar las incógnitas para que la inecuación sea cierta?
Damos valores arbitrarios a la incógnita x, obteniendo:
Para x = 1: 2 · 1 + 1 = 3 < 9
Para x = 2: 2 · 2 + 1 = 5 < 9
Para x = 3: 2 · 3 + 1 = 7 < 9
Para x = 4: 2 · 4 + 1 = 9
Para x = 5: 2 · 5 + 1 = 11 > 9
Por tanto, la inecuación es cierta cuando sustituimos x por un número mayor que 4. La solución es x > 4.
VALOR ABSOLUTO
Valor absoluto de un número real a, se escribe |a|, es el mismo número a cuando es positivo o cero, y opuesto de a, si a es negativo.

PROPIEDADES DEL VALOR ABSOLUTO
1 Los números opuestos tienen igual valor absoluto.
|a| = |−a|
|5| = |−5| = 5
|a · b| = |a| ·|b|
|5 · (−2)| = |5| · |(−2)| |− 10| = |5| · |2| 10 = 10
|a + b| ≤ |a| + |b|
|5 + (−2)| ≤ |5| + |(−2)| |3| = |5| + |2| 3 ≤ 7
ECUACIONES E INECUACIONES CON VALOR ABSOLUTO
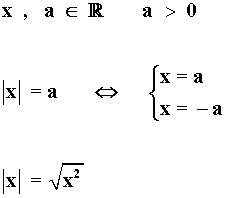
ejemplo:
|1 + 5x| = - 3
Sabemos que siempre tiene que ser:|1 + 5x| ≥ 0 ∀x ∈ R
Luego nunca puede ocurrir:
|1 + 5x| = - 3
Por tanto, la ecuación no tiene solución
EJEMPLO DE INECUACIONES CON VALOR ABSOLUTO
1) |x - 3| > 1
x - 3 < - 1 ó x - 3 > 1
x - 3 < - 1 ⇔ x < - 1 + 3 ⇔ x < 2
x - 3 > 1 ⇔ x > 1 + 3 ⇔ x > 4
x ∈ (-∞ , 2) ∪ (4 , ∞)
2) |x - 3| < 1
- 1 < x - 3 < 1
- 1 + 3 < x < 1 + 3
2 < x < 4
x ∈ (2 ,4)



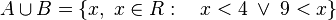


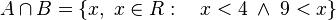



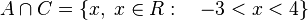






No hay comentarios:
Publicar un comentario