RESEÑA HISTORICA

Inicialmente, una función se identificaba a efectos prácticos con una expresión analítica que permitía calcular sus valores. Sin embargo, esta definición tenía algunas limitaciones: expresiones distintas pueden arrojar los mismos valores, y no todas las «dependencias» entre dos cantidades pueden expresarse de esta manera. En 1837 Dirichlet propuso la definición moderna de función numérica como una correspondencia cualquiera entre dos conjuntos de números, que asocia a cada número en el primer conjunto un único número del segundo.
La intuición sobre el concepto de función también evolucionó. Inicialmente la dependencia entre dos cantidades se imaginaba como un proceso físico, de modo que su expresión algebraica capturaba la ley física que correspondía a este. La tendencia a una mayor abstracción se vio reforzada a medida que se encontraron ejemplos de funciones sin expresión analítica o representación geométrica sencillas, o sin relación con ningún fenómeno natural; y por los ejemplos «patológicos» como funciones continuas sin derivada en ningún punto.
Durante el siglo XIX Julius Wilhelm Richard Dedekind, Karl Weierstrass,partiendo de un estudio profundo de los números reales, desarrollaron la teoría de funciones, siendo esta teoría independiente del sistema de numeración empleado.Con el desarrollo de la teoría de conjuntos, en los siglos XIX y XX surgió la definición actual de función, como una correspondencia entre dos conjuntos de objetos cualesquiera, no necesariamente numéricos.5 También se asoció con otros conceptos vinculados como el de relación binaria.
PAR ORDENADO
es un conjunto de dos elementos A y B que tiene un orden al elemento a se lo llama primera componente y al elemento b se lo llama segunda componente .se lo representa simbólicamente (A, B)
ternaordenado (A,B,C).
PRODUCTO CARTESIANO
sea dos conjuntos A y B no vacíos denominaremos producto cartesiano entre A y B al conjunto de todos los pares ordenados cuya primera componente pertenece al conjunto A y la segunda pertenece al conjunto B simbólicamente se lo representa AxB
EJEMPLO
A={1,2,3}
B=¨{n,v,a}
AxB={(1,n),(1,v),(1,a),(2,n)(2,v),(2,a),(3,n),(3,v),(3,a)}
RELACIONES BINARIAS
una relación establece la correspondencia entre los elementos de dos conjuntos no vacíos A y B. generalmente al conjunto A se lo llama conjunto de partida y al conjunto B ,de llegada simbólicamente se lo representa así R⊆AXB
GRÁFICAS DE RELACIONES R EN R
FUNCIONES DE VARIABLE REAL
DEFINICIÓN DE UNA FUNCIÓN
una función matemática es la correspondencia o relación f de los elementos de un conjunto A con los elementos de un conjunto B.
Una función cumple con la condición de existencia (todos los elementos
de A están relacionados con los elementos de B) y con la condición de
unicidad (cada elemento de A está relacionado con un único elemento de
B).
EJEMPLO:
f(x)= x2 - 5x + 6 D=R
EJEMPLO:


EJEMPLO:

RANGO DE UNA FUNCIÓN
sea f función de variable real f: x->y , el conjunto de todas las imagenes de los elementos del dominio ,constituye el rango de la función .se representa simbólicamente Rg f .
PROCEDIMIENTO:
1.-despejar x
2.-el rango sera el conjunto de valores que tome la variable y.
EJEMPLO:

EJEMPLO:

TIPOS DE FUNCIONES
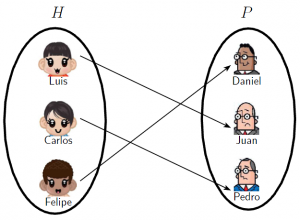
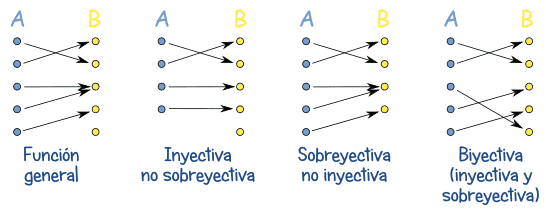 "Inyectivo" significa que cada elemento de "B" tiene como mucho uno de "A" al que corresponde (pero esto no nos dice que todos los elementos de "B" tengan alguno en "A").
"Inyectivo" significa que cada elemento de "B" tiene como mucho uno de "A" al que corresponde (pero esto no nos dice que todos los elementos de "B" tengan alguno en "A").
"Sobreyectivo" significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno). "Biyectivo" significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.
(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo
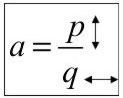
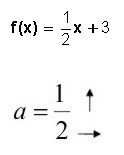

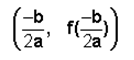

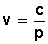
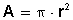
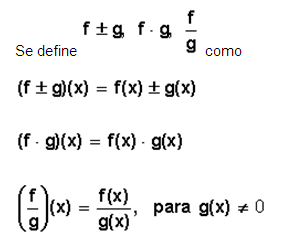

Inyectivo, sobreyectivo y biyectivo" te dan información sobre el comportamiento de una función.
Puedes entender una función como una manera de conectar elementos de un conjunto "A" a los de otro conjunto "B": 
"Sobreyectivo" significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno). "Biyectivo" significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.
DEFINICIONES FORMALES
Inyectivo
Ejemplo: f(x) = x2 del conjunto de los números naturales  a
a  es una función inyectiva.
es una función inyectiva.
(Pero f(x) = x2 no es inyectiva cuando es desde el conjunto de enteros 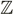 (esto incluye números negativos) porque tienes por ejemplo
(esto incluye números negativos) porque tienes por ejemplo
- f(2) = 4 y
- f(-2) = 4)
Nota: inyectiva también se llama "uno a uno", pero esto se confunde porque suena un poco como si fuera biyectiva.
Sobreyectivo (o también "epiyectivo")
Ejemplo: la función f(x) = 2x del conjunto de los números naturales  al de los números pares no negativos es sobreyectiva.
al de los números pares no negativos es sobreyectiva.
Sin embargo, f(x) = 2x del conjunto de los números naturales a
a  no es sobreyectiva, porque, por ejemplo, ningún elemento de
no es sobreyectiva, porque, por ejemplo, ningún elemento de  va al 3 por esta función.
va al 3 por esta función.
Sin embargo, f(x) = 2x del conjunto de los números naturales
Biyectiva
(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo
- f(2)=4 y
- f(-2)=4)
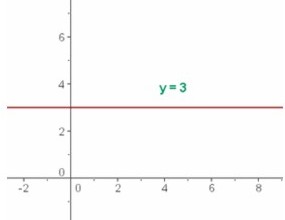
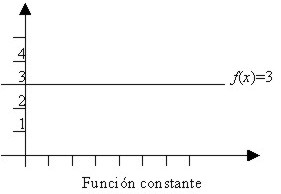
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.


FUNCION LINEAL
Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales son funciones polinómicas.
Ejemplo:
F(x) = 2x - 1
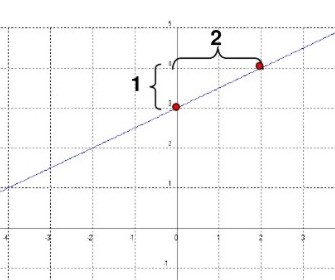
Es una función lineal con pendiente m = 2 e intercepto en y en (0, -1). Su gráfica es una recta ascendente.


Para trazar la gráfica de una función lineal solo es necesario conocer dos de sus puntos.
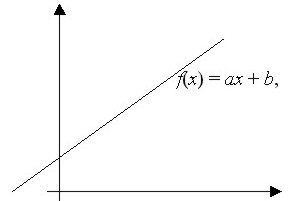
La ecuación matemática que representa a esta función, como ya vimos, es f(x) = ax + b, donde f(x) corresponde al valor de y, entonces
y = ax + b
Donde "a" es la pendiente de la recta, y "b" es la ordenada al origen.
La pendiente indica la inclinación de la recta, cuanto sube o baja y cuanto avanza o retrocede. Esto depende del signo que tenga.
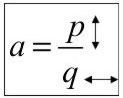
El valor de "a" siempre es una fracción (si no tiene nada abajo, es porque tiene un 1), donde el numerador (p) me indica cuanto sube o baja, y el denominador (q) indica cuanto avanzo o retrocedo.
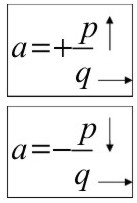
Aprendido esto, y según el signo de la fracción, la pendiente se marca de la siguiente forma:

La ordenada al origen (b) es el valor donde la recta corta al eje y.
La recta siempre va a pasar por el punto (0; b)
Representación gráfica de una función lineal o función afín
Para graficar una recta, alcanza con los datos que da la ecuación matemática de la función, y se opera de la siguiente manera:
- 1. Se marca sobre el eje y la ordenada al origen, el punto por donde la recta va a cortar dicho eje.
- 2. Desde ese punto, subo o bajo según sea el valor de "p" y avanzo o retrocedo según indique el valor de "q". En ese nuevo lugar, marco el segundo punto de la recta.
- 3. Se podría seguir marcando puntos con la misma pendiente, pero con 2 de ellos ya es suficiente como para poder graficar la recta.
- 4. Teniendo ya los dos puntos, con regla se traza la recta que pasa por los mismos.
Ejemplo:
Graficar la siguiente función:
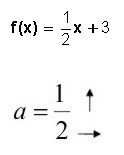
La ordenada al origen (3) me indica que me debo parar sobre el eje y en el 3.

También podemos graficar una función dando valores a x y obteniendo dos puntos en las coordenadas.
Ejemplo:
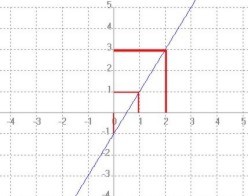
Graficar la función dada por f(x) = 2x – 1
Solución
Como la función es lineal se buscan dos puntos de la recta; para ello, se le dan valores a x y se encuentran sus imágenes respectivas, esto es:
Si x = 0, se tiene que f (0) = 2(0) – 1 = - 1
Si x = 2, se tiene que f (2) = 2(2) – 1 = 3
Así, los puntos obtenidos son (0, -1) y (2, 3), por los cuales se traza la gráfica correspondiente.
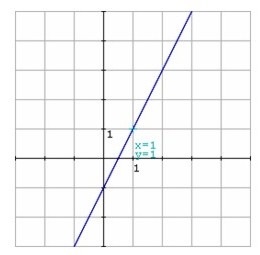 |
FUNCION POLINOMICA

El dominio de todas estas funciones polinómicas es el conjunto de los números reales (porque el elemento x puede ser cualquier número real).
FUNCION CUADARTICA
Una función de la forma f(x) = ax2 + bx + c, donde a, b y c son constantes y a es diferente de cero, se conoce como una función cuadrática.
La representación gráfica de una función cuadrática es una parábola. Una parábola abre hacia arriba si a > 0 y abre hacia abajo si a < 0. El vértice de una parábola se determina por la fórmula:
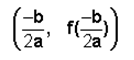
Las funciones cuadráticas son funciones polinómicas.
Ejemplo:
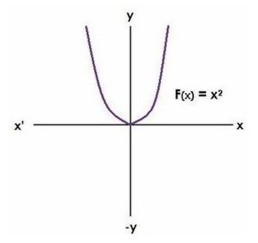 |
F(x) = x2 representa una parábola que abre hacia arriba con vértice en (0,0).
|
FUNCION RACIONAL
Una función racional es el cociente de dos funciones polinómicas. Así es que q es una función racional si para todo x en el dominio, se tiene:

Nota: El dominio de una función polinómica son los números reales; sin embargo, el dominio de una función racional consiste de todos los números reales excepto los ceros del polinomio en el denominador (ya que la división por cero no está definida).
Función de potencia
Una función de potencia es toda función de la forma f(x) = xr, donde r es cualquier número real.
Las funciones f(x) = x4/3 y h(x) = 5x3/2 son funciones de potencia.
Ejercicios y ejemplos con funciones en general:
Expresar mediante una fórmula la función que asocia a cada número:
a) Su cuádruplo.
La función es: f (x) = 4x.
b) Un número 2 unidades mayor.
La función es: f (x) = x + 2.
c) Su mitad menos 1.
La función es: f (x) = x/2 - 1.
d) El cuadrado del número que es una unidad menor.
La función es: f (x) = (x - 1)2
Veamos algunos otros ejemplos de funciones:
1) El volumen de un gas está determinado por la presión (a temperatura constante), esta relación viene dada por la ley de Boyle-Mariotte:
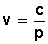
Donde v representa el volumen del gas en litros, p es la presión en atmósferas y c es una constante de proporcionalidad.
Se observa que al variar la presión a la que está sometido el gas varía el volumen; es decir, los valores del volumen dependen de los valores de la presión del gas y para cada valor de la presión existe un único valor del volumen.
2) El área A del círculo depende de la longitud de su radio r y está dada por la fórmula:
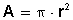
Si se conoce el valor del radio se puede conocer el valor del área del círculo.
3) Dada la función f(x) = 5x2 + 2
Encontrar el valor de la función para cuando x = 2.
Para calcular la imagen de un elemento bajo la función f, se reemplaza dicho elemento en el lugar de la variable, así para x = 2
F (2) = 5(2)2 + 2
F (2) = 22
Por lo tanto cuando x = 2, se tiene que f (2) = 22.
Ejemplo:
El precio de arrendar un auto es de 15 dólares más 0,20 de dólar por kilómetro recorrido.
- a) Hallar la fórmula que expresa el costo del arriendo en función del número de los kilómetros recorridos.
- b) ¿Cuánto hay que pagar si se han recorrido 50 kilómetros?
c) Si han cobrado 53 dólares ¿cuántos kilómetros se han recorrido?
Veamos:
a) Si llamamos x al número de kms recorridos, la fórmula de la función es f (x) = 15 + 0,2x.
b) x = 50 entonces
F (50) = 15 + 0,2 • 50 = 25
Hay que pagar 25 dólares.
c) f (x) = 53 entonces
15 + 0,2x = 53 entonces x = 190
Se han recorrido 190 km.
Álgebra de funciones
Suma, resta, multiplicación y división de funciones
Sean f y g dos funciones cualesquiera.
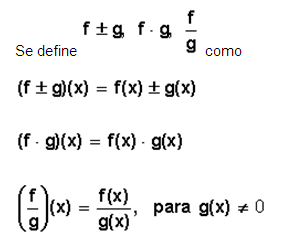
Ejemplos:
Suma de funciones
Sean las funciones

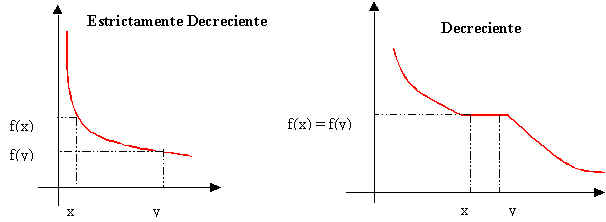
FUNCIÓN MONÓTONA
Se dice que F es una función monótona en un intervalo I , si y solo si F es estrictamente creciente o estrictamente decreciente en ese intervalo.

CLASIFICACIÓN DE LAS FUNCIONES
Funciones algebraicas
TÉCNICAS DE GRAFICACION
PROCESO DE GRAFICACION DE UNA FUNCIÓN
Ejemplos
- La gráfica de la función

- es {(1,a), (2,b), (3,c)}.
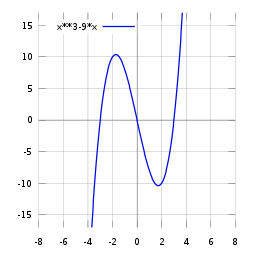
- La gráfica del polinomio cúbico en la recta real

- es {(x,x3-9x) : donde x es un número real}. Si el conjunto se representa en un plano cartesiano, el resultado es como el de la imagen.
TRAZADO DE GRAFICAS ESPECIALES
para los cortes Y se utiliza  ejemplos
ejemplos
 ejemplos
ejemplos
(A>o)^(b>0)

b) ; (a>o)^(b>0)
OPERACIONES CON FUNCIONES

APLICACIONES
1. Un algodonero recoge 30 Kg cada hora, y demora media hora preparándose todos los días cuando inicia la jornada. La función lineal que representa esta situación es y = 30x – 15 donde y representa los Kg de algodón recogido y x el tiempo transcurrido en horas.
y luego graficamos

APLICACIONES
1. Un algodonero recoge 30 Kg cada hora, y demora media hora preparándose todos los días cuando inicia la jornada. La función lineal que representa esta situación es y = 30x – 15 donde y representa los Kg de algodón recogido y x el tiempo transcurrido en horas.
Realiza una tabla para la anterior función y grafícala.
¿Cuantos Kg de algodón se recogerán en una jornada de 8 horas?
Primero realizamos la tabla.
x
(tiemp en horas)
|
y
(Kg algodón)
|
0.5
|
0
|
1
|
15
|
1.5
|
30
|
2
|
45
|


 , es decir, cualquier número real tiene imagen.
, es decir, cualquier número real tiene imagen.




No hay comentarios:
Publicar un comentario