Matemáticas para sistemas: TRIGONOMETRIA

RESEÑA HISTORICA

La historia de la trigonometría comienza con los babilonios y los egipcios. Estos últimos establecieron la medida de los ángulos en grados, minutos y segundos. Sin embargo, en los tiempos de la Grecia clásica, en el siglo II a.C. el astrónomo Hiparco de Nicea construyó una tabla de cuerdas para resolver triángulos. Comenzó con un ángulo de 71° y yendo hasta 180° con incrementos de 71°, la tabla daba la longitud de la cuerda delimitada por los lados del ángulo central dado que corta a una circunferencia de radio r. No se sabe el valor que Hiparco utilizó para r.
Tres siglos después, el astrónomo Claudio Ptolomeo utilizó r = 60, pues los griegos adoptaron el sistema numérico base 60 de los babilonios.
Durante muchos siglos, la trigonometría de Ptolomeo fue la introducción básica para los astrónomos. Su libro de Astronomía, el Almagesto, también tenía una tabla de cuerdas junto con la explicación de su método para compilarla, y a lo largo del libro mostraba ejemplos de cómo utilizar dicha tabla para calcular los elementos desconocidos de un triángulo a partir de los conocidos. El Teorema de Menelao utilizado para resolver triángulos esféricos fue autoría de Ptolomeo.
Al mismo tiempo, los astrónomos de la India habían desarrollado también un sistema trigonométrico basado en la función seno en vez de cuerdas como los griegos. Esta función seno, era la longitud del lado opuesto a un ángulo en un triángulo rectángulo de hipotenusa dada. Los matemáticos hindúes utilizaron diversos valores para ésta en sus tablas.
A finales del siglo VIII los astrónomos árabes trabajaron con la función seno y a finales del siglo X ya habían completado la función seno y las otras cinco funciones. También descubrieron y demostraron teoremas fundamentales de la trigonometría, tanto para triángulos planos como esféricos. Los matemáticos sugirieron el uso del valor r = 1 en vez de r = 60, y esto dio lugar a los valores modernos de las funciones trigonométricas
El Occidente latino se familiarizó con la trigonometría árabe a través de traducciones de libros de astronomía arábigos, que comenzaron a aparecer en el siglo XII. El primer trabajo importante en esta materia en Europa fue escrito por el matemático y astrónomo alemán Johann Müller Königsberg, llamado Regiomontano.
A principios del siglo XVII, el matemático escocés John Napier descubrió los logaritmos y, gracias a esto, los cálculos trigonométricos recibieron un gran empuje.
A mediados del siglo XVII, los científicos Isaac Newton y Gottfried Wilhelm Leibniz desarrollaron el Cálculo diferencial e integral. Uno de los fundamentos del trabajo de Newton fue la representación de muchas funciones matemáticas utilizando series infinitas de potencias de la variable x. Newton encontró la serie para sen x y series similares para cos x y tg x. Con la invención del Cálculo, las funciones trigonométricas fueron incorporadas al Análisis, donde todavía hoy desempeñan un importante papel tanto en las matemáticas puras como en las aplicadas.
Por último, en el siglo XVIII, el matemático suizo Leonhard Euler demostró que las propiedades de la trigonometría eran producto de la aritmética de los números complejos y, además, definió las funciones trigonométricas utilizando expresiones con exponenciales de números complejos.

ANGULOS Y SUS MEDIDAS

Ángulo es la región del plano comprendida entre dos semirrectas
(lados) que tienen el mismo origen (vértice).
Notación: â o bien
Los ángulos se miden en grados.

ÁNGULOS COMPLEMENTARIOS Y ÁNGULOS SUPLEMENTARIOS

Ángulos complementarios son los que suman un recto (90º)
Ángulos suplementarios son los que suman un llano (180º)

angulocomplementario angulo suplementario

Complementario de â = ê
Complementario de ê = â
Suplementario de î = ô
Suplementario de ô = î

ÁNGULOS CONSECUTIVOS Y ÁNGULOS OPUESTOS POR EL VÉRTICE

Dos ángulos son consecutivos si tienen el mismo vértice y un lado en común.
Dos ángulos son opuestos por el vértice si tienen el mismo vértice y los lados de uno
son la prolongación de los del otro.

UNIDADES ANGULARES
En la medida de ángulos, y por tanto en trigonometría, se emplean tres unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografia, arquitectura o en construccion.
Radián: unidad angular natural en trigonometría, será la que aquí utilicemos, en una circunferencia completa hay 2π radianes.
Grado sexagesimal: unidad angular que divide una circunferencia en 360º.
Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.

LONGITUD DE UNA CIRCUNFERENCIA

La longitud de la circunferencia es igual al producto de su diámetro por el
número .

L = d .π
L = 2π r

EJEMPLO

1º Calcular la longitud de una rueda de 90 cm de diámetro.

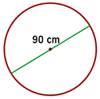
1º A partir del diámetro

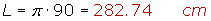
2º A partir del radio

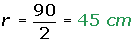
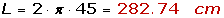
EJEMPLO:

4ºLa longitud de una circunferencia es 43.96 cm. ¿Cuál es el área del círculo?

LOS RADIANES CON SUS FUNCION

FUNCIONES TRIGONOMETRICAS

FUNCIONES

IDENTIDADES TRIGONOMETRICAS

Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones. Notación: se define sin²α como ². Lo mismo se aplica a las demás funciones trigonométricas.