RESEÑA HISTORICA
CLASES DE MATRICES
MATRIZ FILA
es una sola fila es decir su orden es de 1xn
A=1*4 
MATRIZ COLUMNA es una matriz formada por una sola columna
A=
MATRIZ RECTANGULAR
es una matriz que tiene el numero de fila diferente al de las colimnas es decir su orden es m x n
A=3*2
MATRIZ CUADRADA
La matriz cuadrada tiene el mismo número de filas que de columnas.
Los elementos de la forma aii constituyen la diagonal principal.
La diagonal secundaria la forman los elementos con i+j = n+1.
A=3*3
CONCEPTOS ASICIADOS ALA MATRIZ
DIAGONAL PRINCIPAL: la constiye la diaginal aij en donde i=j
LA TRAZA :es la suma de los elementos de la diagonal principal y se denota TR(A)=1a
DIAGONAL SECUNDARIA :la comstituye los elementos de aij que cumplen com la condicion aij+n+1
Amxn
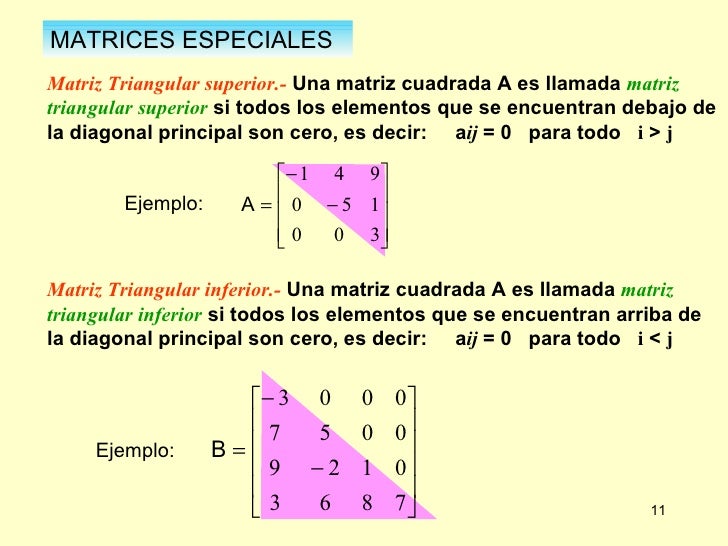
MATRIZ TRIANGULAR SUPERIOR: es una matriz cuadrada que tiene tidos los elementos bajo el diaginal principal iguales a 0 esto es aij=0 si i es mayor que j
MATRIZ NULA : es una matriz que todos los elementos es iagual a 0
0mxn
MATRIZ DIAGONAL : es una matriz cuadrada que tiene todos sus elementos sibre y bajo la diaginal principal iguales a 0 esti es aij=0 si i
MATRIZ IDENTIDAD : es una matriz cuadrada que tiene tidis sus elementos igualesa 0 exesti los de la diaginales a1 y se denota mxn
CLASIFICACION DE MATRICES
Triangular superior
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.
Triangular inferior
En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros
Diagonal
En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.
En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.
Escalar
Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
Identidad
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Potencia
Se llama potencia k-ésima de una matriz cuadrada A, donde k OE Õ, un entero positivo, al producto de A por sí misma, repetido k veces.
Ak =A⋅A⋅A⋅......k veces ...... ⋅A
Se conviene en que:
A- k = (A- 1) k " k OE Õ
A0 = I
Periodica
Se llama potencia k-ésima de una matriz cuadrada A, donde k OE Õ, un entero positivo, al producto de A por sí misma, repetido k veces.
Ak =A⋅A⋅A⋅......k veces ...... ⋅A
Se conviene en que:
A- k = (A- 1) k " k OE Õ
A0 = I
Periodica
si
. Si p es el menor número natural que satisface 
, entonces decimos que A es una matriz periódica de período
Nilpotente
Si A es una matriz cuadrada y Ak = 0 para algún número natural k, se dice que A es nilpotente. Si k es tal que Ak −1 ≠ 0 y Ak = 0, se dice que A es nilpotente de orden k.
Idempotente
Una matriz, A, es idempotente si:
A2 = A.
Involutiva
Una matriz, A, es involutiva si:
A2 = I.
Traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas
Si A es una matriz cuadrada y Ak = 0 para algún número natural k, se dice que A es nilpotente. Si k es tal que Ak −1 ≠ 0 y Ak = 0, se dice que A es nilpotente de orden k.
Idempotente
Una matriz, A, es idempotente si:
A2 = A.
Involutiva
Una matriz, A, es involutiva si:
A2 = I.
Traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas
(At)t = A
(A + B)t = At + Bt
(α ·A)t = α· At
(A · B)t = Bt · AtSimétrica
Una matriz simétrica es una matriz cuadrada que verifica:
A = At.Antisimetrica
Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica:
A = -At.
Compleja
Sus elementos son números complejos aij e ¬
Conjugada
Matriz conjugada de una matriz A Aquella que se obtiene sustituyendo cada elemento por su complejo conjugado (igual parte real, pero la parte imaginaria cambiada de signo)Hermitiana o hermitica
Una matriz hermitiana (o hermítica) es una matriz cuadrada de elementos complejos que tiene la característica de ser igual a su propia traspuesta conjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los índices i y j:
(A + B)t = At + Bt
(α ·A)t = α· At
(A · B)t = Bt · AtSimétrica
Una matriz simétrica es una matriz cuadrada que verifica:
A = At.Antisimetrica
Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica:
A = -At.
Compleja
Sus elementos son números complejos aij e ¬
Conjugada
Matriz conjugada de una matriz A Aquella que se obtiene sustituyendo cada elemento por su complejo conjugado (igual parte real, pero la parte imaginaria cambiada de signo)Hermitiana o hermitica
Una matriz hermitiana (o hermítica) es una matriz cuadrada de elementos complejos que tiene la característica de ser igual a su propia traspuesta conjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los índices i y j:
o, escrita con la traspuesta conjugada A*:
Por ejemplo,
es una matriz hermítica.
Antihermitiana
una Matriz antihermitiana es una matriz cuadrada cuya traspuesta conjugada es menos la matriz. Esto es si satisface a la relación:
A * = -A
Antihermitiana
una Matriz antihermitiana es una matriz cuadrada cuya traspuesta conjugada es menos la matriz. Esto es si satisface a la relación:
A * = -A
o en su forma componente, si (A = ai,j):
Para todas las i y las j.
Ortogonal
Una matriz ortogonal es necesariamente cuadrada e invertible : A-1 = AT La inversa de una matriz ortogonal es una matriz ortogonal. El producto de dos matrices ortogonales es una matriz ortogonal. El determinante de una matriz ortogonal vale +1 ó -1.
PROPIEDAES DE LAS MATRICES
1. Interna
La suma de dos matrices de orden m x n es otra matriz dimensión m x n.
2. Asociativa
A + (B + C) = (A + B) + C
3. Elemento neutro
A + 0 = A
Donde O es la matriz nula de la misma dimensión que la matriz A.
4. Elemento opuesto
A + (−A) = O
La matriz opuesta es aquella en que todos los elementos están cambiados de signo.
5. Conmutativa
A + B = B + A
OPERACIONES ENTRE MATRICES
IGUALDAD DE MATRICES
Dos
matrices son iguales si tienen las
mismas dimensiones y cada elemento de la primera es igual al elemento de la
segunda que ocupa su misma posición. Es decir:
Mm,n
Ejemplo:
SUMA DE MATRICES
Dadas dos matrices de la misma dimensión, A=(aij) y B=(bij), se define la matriz suma como: A+B=(aij+bij).
La matriz suma se obtienen sumando los elementos de las dos matrices que ocupan la misma misma posición.
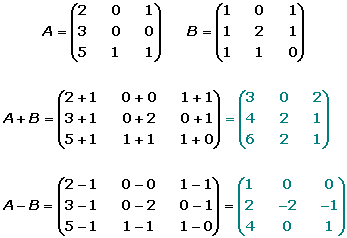
DIFERENCIA DE MATRICES
Sean
Mm,n
dos matrices de la misma dimensión. Se define la matriz 
como la suma de 
con la opuesta de 
.
Es decir,
Mm,n
dos matrices de la misma dimensión. Se define la matriz
como la suma de
con la opuesta de .
Es decir,PRODUCTO DE UNA MATRIZ
Dadas
las matrices A de dimensión m x n
y B de dimensión n x p
se define la matriz producto C de dimensión
m x p
como aquella cuyo elemento 
se obtiene multiplicando la i-esima fila de la matriz A por la k-esima columna
de la matriz B. Es decir:
se obtiene multiplicando la i-esima fila de la matriz A por la k-esima columna
de la matriz B. Es decir:
Mm,p
; 
,
POTENCIA DE MATRICES
DETERMINANTES
DETERMINANTE DE UNA MATRIZ
METODO PARA ENCONTRAR LA DETERMINANTE DE UNA MATRIZ
No hay comentarios:
Publicar un comentario